Den Sinus mit Excel richtig berechnen

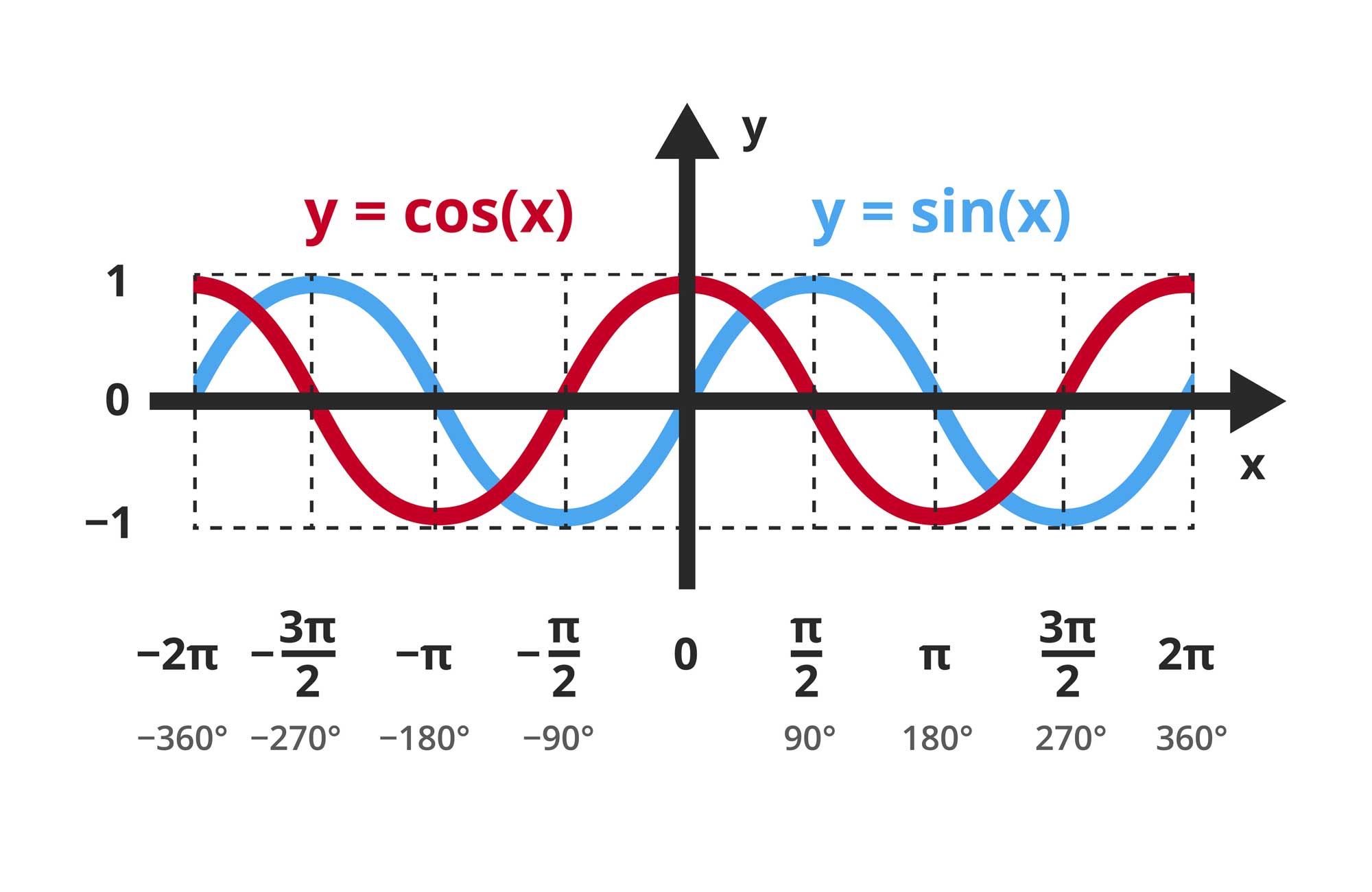
Die Funktionen zur Berechnung des Sinus lautet in Excel "SIN".

Wenn Sie jetzt jedoch einfach die Gradzahl eingeben, wird Excel Ihnen einen falschen Wert liefern. Ich nehme mal als Beispiel 50°.

Die Formel =SIN(50) liefert den Wert -0,262374854.
Der richtige Wert wäre jedoch 0,766044443.

Woran liegt das?
Excel rechnet nicht mit dem Winkel sondern mit dem so genannten Bogenmaß.

Für eine Umrechnung muss der gesuchte Wert durch 180 dividiert werden und dann mit der Zahl Pi multipliziert:

• Die Zahl Pi entspricht der Zahl 3,141592654.
• Auch für die Zahl PI gibt es eine Funktion in Excel, diese lautet PI().
• Die komplette Formel lautet dann also =SIN(50/180*PI()). Diese Formel liefert Ihnen dann immer das richtige Ergebnis.

PS: Qualitätsmanagement ist uns wichtig!

Bitte teilen Sie uns mit, wie Ihnen unser Beitrag gefällt. Klicken Sie hierzu auf die unten abgebildeten Sternchen (5 Sternchen = sehr gut):

PPS: Ihnen hat der Beitrag besonders gut gefallen?

Unterstützen Sie unser Ratgeberportal: